[프로그래머스] 카드 짝 맞추기 (Python)
- -
Problem : 코딩테스트 연습 - 카드 짝 맞추기 | 프로그래머스 스쿨 (programmers.co.kr)
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
Status : Solved
Time : 01:35:29
문제 설명
게임 개발자인 베로니는 개발 연습을 위해 다음과 같은 간단한 카드 짝맞추기 보드 게임을 개발해 보려고 합니다.
게임이 시작되면 화면에는 카드 16장이 뒷면을 위로하여 4 x 4 크기의 격자 형태로 표시되어 있습니다. 각 카드의 앞면에는 카카오프렌즈 캐릭터 그림이 그려져 있으며, 8가지의 캐릭터 그림이 그려진 카드가 각기 2장씩 화면에 무작위로 배치되어 있습니다.
유저가 카드를 2장 선택하여 앞면으로 뒤집었을 때 같은 그림이 그려진 카드면 해당 카드는 게임 화면에서 사라지며, 같은 그림이 아니라면 원래 상태로 뒷면이 보이도록 뒤집힙니다. 이와 같은 방법으로 모든 카드를 화면에서 사라지게 하면 게임이 종료됩니다.
게임에서 카드를 선택하는 방법은 다음과 같습니다.
- 카드는 커서를 이용해서 선택할 수 있습니다.
- 커서는 4 x 4 화면에서 유저가 선택한 현재 위치를 표시하는 "굵고 빨간 테두리 상자"를 의미합니다.
- 커서는 [Ctrl] 키와 방향키에 의해 이동되며 키 조작법은 다음과 같습니다.
- 방향키 ←, ↑, ↓, → 중 하나를 누르면, 커서가 누른 키 방향으로 1칸 이동합니다.
- [Ctrl] 키를 누른 상태에서 방향키 ←, ↑, ↓, → 중 하나를 누르면, 누른 키 방향에 있는 가장 가까운 카드로 한번에 이동합니다.
- 만약, 해당 방향에 카드가 하나도 없다면 그 방향의 가장 마지막 칸으로 이동합니다.
- 만약, 누른 키 방향으로 이동 가능한 카드 또는 빈 공간이 없어 이동할 수 없다면 커서는 움직이지 않습니다.
- 커서가 위치한 카드를 뒤집기 위해서는 [Enter] 키를 입력합니다.
- [Enter] 키를 입력해서 카드를 뒤집었을 때
- 앞면이 보이는 카드가 1장 뿐이라면 그림을 맞출 수 없으므로 두번째 카드를 뒤집을 때 까지 앞면을 유지합니다.
- 앞면이 보이는 카드가 2장이 된 경우, 두개의 카드에 그려진 그림이 같으면 해당 카드들이 화면에서 사라지며, 그림이 다르다면 두 카드 모두 뒷면이 보이도록 다시 뒤집힙니다.
- [Enter] 키를 입력해서 카드를 뒤집었을 때
"베로니"는 게임 진행 중 카드의 짝을 맞춰 몇 장 제거된 상태에서 카드 앞면의 그림을 알고 있다면, 남은 카드를 모두 제거하는데 필요한 키 조작 횟수의 최솟값을 구해 보려고 합니다. 키 조작 횟수는 방향키와 [Enter] 키를 누르는 동작을 각각 조작 횟수 1로 계산하며, [Ctrl] 키와 방향키를 함께 누르는 동작 또한 조작 횟수 1로 계산합니다.
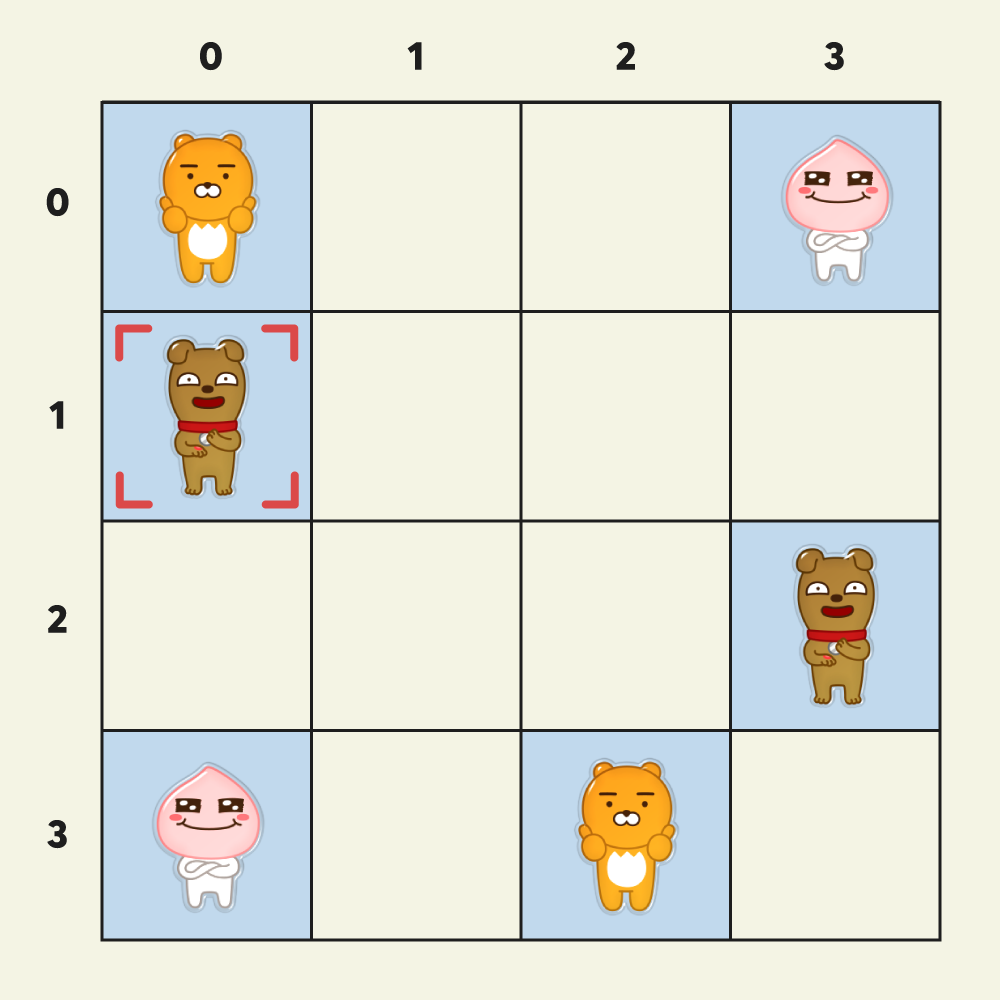
* 문제 예시는 위 링크를 참고해 주세요!
현재 카드가 놓인 상태를 나타내는 2차원 배열 board와 커서의 처음 위치 r, c가 매개변수로 주어질 때, 모든 카드를 제거하기 위한 키 조작 횟수의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
입력 및 출력
제한사항
- board는 4 x 4 크기의 2차원 배열입니다.
- board 배열의 각 원소는 0 이상 6 이하인 자연수입니다.
- 0은 카드가 제거된 빈 칸을 나타냅니다.
- 1 부터 6까지의 자연수는 2개씩 들어있으며 같은 숫자는 같은 그림의 카드를 의미합니다.
- 뒤집을 카드가 없는 경우(board의 모든 원소가 0인 경우)는 입력으로 주어지지 않습니다.
- r은 커서의 최초 세로(행) 위치를 의미합니다.
- c는 커서의 최초 가로(열) 위치를 의미합니다.
- r과 c는 0 이상 3 이하인 정수입니다.
- 게임 화면의 좌측 상단이 (0, 0), 우측 하단이 (3, 3) 입니다.
입출력 예
| board | r | c | result |
| [[1,0,0,3],[2,0,0,0],[0,0,0,2],[3,0,1,0]] | 1 | 0 | 14 |
| [[3,0,0,2],[0,0,1,0],[0,1,0,0],[2,0,0,3]] | 0 | 1 | 16 |
풀이
탐색 문제 난이도 중상. 시작 좌표에서부터 탐색을 진행하되, 카드 쌍을 뒤집거나 그 쌍 중 하나를 뒤집는 등의 정보 변화가 존재하므로 이를 반영하는 코드가 필요하다.
- ctr_move : ctrl + 방향키 이동 시 최종적으로 도달하는 좌표를 반환하는 함수이다.
- check_move : 큐에 삽입할 다음 정보를 계산하고, 큐에 삽입할지 여부를 결정하는 함수이다. 이미 카드 한 장을 열어본 상태(즉 다른 카드 쌍을 찾아야 할 때)와 그렇지 않은 상태로 크게 나뉜다. 각 경우에 따라 다음 목표 좌표와 카드를 열어볼 지 말지에 대한 정보가 달라지므로, 이에 대한 조건을 전부 따져 큐에 삽입한다. 이미 지나온 좌표를 다시 지나치는 경우를 베제하기 위하여, tot_visited에 저장된 최소 이동 거리와 비교하여 최소인 경우에만 큐에 삽입한다.
- find_max_visited : 문제에 나올 수 있는 카드 쌍은 최대 6쌍이며, board에 주어진 카드 쌍을 모두 방문하였을 때의 경우를 반환하게 된다. 이는 나중에 탐색 시 결과를 갱신하는 데 쓰인다.
- make_card_dict : 카드 쌍 하나를 열게 되면, 다른 하나의 좌표 정보가 필요하게 된다. 이를 위해 한 쌍의 한 좌표를 넣었을 때 다른 좌표를 반환하는 dictionary를 작성하는 함수를 만들었다. board를 탐색하여 각 쌍에 대한 좌표를 저장한 후, 각 쌍에 대한 서로의 좌표를 반환할 수 있는 dictionary를 작성하여 반환하도록 한다.
- solution : main함수. 위 함수들을 이용하여 DFS로 탐색하는 코드를 구현하였다. 이 때 tot_visited는 (현재 target, 이때까지 완료한 카드 쌍 visited, 현재 x, y)좌표를 저장하는 4차원 배열이다(개인적으로 좋지 않은 구조라고 생각한다). 현재 좌표에서 상하좌우로 한 칸씩 움직일 때, 그리고 ctrl을 적용하였을 때의 총 8가지 경우의 좌표 변화를 탐색하고, 그 좌표 변화에 따른 정보 변화를 check_move 함수로 측정한다. 또한 유념해야 할 점은, enter를 누르는 경우의 수는 무조건 (총 쌍의 개수 * 2)로 최적화된다는 점이다.(즉 실패하지 않고 한 번에 모든 쌍을 맞추는 게 최선의 방법이다). 이를 위해 마지막에 (총 쌍의 개수 * 2)를 더해주었다.
풀이 코드
from collections import defaultdict, deque
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
MAX = float('inf')
def ctr_move(board, visited, sx, sy, direct) :
while True :
sx, sy = sx + dx[direct], sy + dy[direct]
if -1 < sx < 4 and -1 < sy < 4 :
if board[sy][sx] and not visited & 1 << board[sy][sx] - 1 :
break
continue
sx, sy = sx - dx[direct], sy - dy[direct]
break
return sx, sy
def check_move(board, ax, ay, dist, q, tot_visited, visited, targeted, target_pos, card_dict) :
next_visited = visited
next_target_pos = target_pos
if targeted and board[ay][ax] == targeted and target_pos == (ax, ay):
next_target = 0
next_visited = visited | (1 << (targeted - 1))
next_target_pos = target_pos
elif targeted :
next_target = targeted
elif board[ay][ax] and not visited & 1 << board[ay][ax] - 1 :
next_target = board[ay][ax]
next_target_pos = card_dict[(ax, ay)]
else :
next_target = 0
if tot_visited[ay][ax][next_target][next_visited] > dist+1 :
tot_visited[ay][ax][next_target][next_visited] = dist+1
q.append((ax, ay, next_visited, next_target, next_target_pos, dist+1))
def find_max_visited(board) :
result = 0
for i in range(4) :
for j in range(4) :
if board[i][j] :
result |= 1 << board[i][j] - 1
return result
def make_card_dict(board) :
tmp = defaultdict(list)
for i in range(4) :
for j in range(4) :
if board[i][j] :
tmp[board[i][j]].append((j,i))
result = dict()
for val in tmp.values() :
result[val[0]] = val[1]
result[val[1]] = val[0]
return result
def solution(board, r, c) :
tot_visited = [[[[MAX]*(1<<6) for _ in range(7)] for _ in range(4)] for _ in range(4)]
tot_visited[c][r][0][0] = 0
result = MAX
max_visited = find_max_visited(board)
max_check = bin(max_visited).count('1') * 2
card_dict = make_card_dict(board)
q = deque([(c, r, 0, 0, (0,0), 0)])
if board[r][c] :
tot_visited[r][c][board[r][c]][0] = 0
q.append((c, r, 0, board[r][c], card_dict[(c,r)], 0))
while q :
x, y, visited, targeted, target_pos, dist = q.popleft()
if visited == max_visited:
result = min(result, dist)
continue
for k in range(4) :
ax, ay = x + dx[k], y + dy[k]
if ax < 0 or ax > 3 or ay < 0 or ay > 3 :
continue
check_move(board, ax, ay, dist, q, tot_visited, visited, targeted, target_pos, card_dict)
ax, ay = ctr_move(board, visited, x, y, k)
check_move(board, ax, ay, dist, q, tot_visited, visited, targeted, target_pos, card_dict)
return result + max_check
p.s. 총 카드 쌍은 기껏해야 6쌍이기에, 순열 및 조합을 통한 풀이도 충분히 실용적일 것이다(이를 이용해 풀이한 다른 코드도 존재함을 확인하였다)
구현 부분에 많은 한계를 느꼈던 문제였다. 맞왜틀도 꽤 많았고, 함수의 계층화 등의 구조 디자인이나 변수명 지정 등의 사소한 문제까지 종합적으로 여러움을 겪었던 것 같다. 문제 자체는 꽤 어렵진 않았던 것 같은데... 실제 협업같은 경험이 부족하여 생기는 문제라고 본다.
실험적으로 코드의 각 함수에 대한 개략적인 설명을 덧붙였는데, 코드 리뷰와 같이 다른 사람들에게 보여주기 위한 설명을 정리하는 것도 위 문제를 해결하기 위한 방안 중 하나고 생각했다. 과연 효과가 있을 진 모르지만, 일단은 이렇게 해 보는 것도 나쁘지 않은 것 같다.
'PS > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 숫자 타자 대회 (Python) (0) | 2023.02.13 |
|---|---|
| [프로그래머스] 셔틀버스 (Python) (0) | 2023.02.11 |
| [프로그래머스] 자물쇠와 열쇠 (Python) (0) | 2023.02.07 |
| [프로그래머스] 퍼즐 조각 채우기 (Python) (0) | 2023.02.06 |
| [프로그래머스 / 카카오 2023] 1차 코딩테스트 해설모음 (Python) (0) | 2023.02.05 |
소중한 공감 감사합니다