[프로그래머스] 블록 게임 (Python)
- -
Problem : https://school.programmers.co.kr/learn/courses/30/lessons/42894
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
Status : Solved
Time : 00:27:34
문제 설명
프렌즈 블록이라는 신규 게임이 출시되었고, 어마어마한 상금이 걸린 이벤트 대회가 개최 되었다.
이 대회는 사람을 대신해서 플레이할 프로그램으로 참가해도 된다는 규정이 있어서, 게임 실력이 형편없는 프로도는 프로그램을 만들어서 참가하기로 결심하고 개발을 시작하였다.
프로도가 우승할 수 있도록 도와서 빠르고 정확한 프로그램을 작성해 보자.
게임규칙
아래 그림과 같이 1×1 크기의 블록을 이어 붙여 만든 3 종류의 블록을 회전해서 총 12가지 모양의 블록을 만들 수 있다.
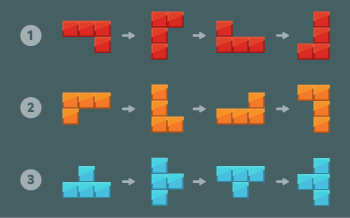
1 x 1 크기의 정사각형으로 이루어진 N x N 크기의 보드 위에 이 블록들이 배치된 채로 게임이 시작된다. (보드 위에 놓인 블록은 회전할 수 없다). 모든 블록은 블록을 구성하는 사각형들이 정확히 보드 위의 사각형에 맞도록 놓여있으며, 선 위에 걸치거나 보드를 벗어나게 놓여있는 경우는 없다.
플레이어는 위쪽에서 1 x 1 크기의 검은 블록을 떨어뜨려 쌓을 수 있다. 검은 블록은 항상 맵의 한 칸에 꽉 차게 떨어뜨려야 하며, 줄에 걸치면 안된다.
이때, 검은 블록과 기존에 놓인 블록을 합해 속이 꽉 채워진 직사각형을 만들 수 있다면 그 블록을 없앨 수 있다.
예를 들어 검은 블록을 떨어뜨려 아래와 같이 만들 경우 주황색 블록을 없앨 수 있다.
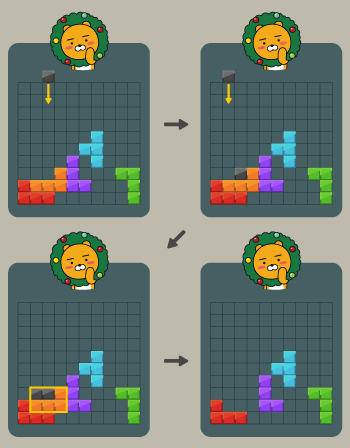
빨간 블록을 가로막던 주황색 블록이 없어졌으므로 다음과 같이 빨간 블록도 없앨 수 있다.
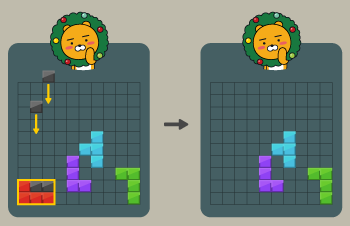
그러나 다른 블록들은 검은 블록을 떨어뜨려 직사각형으로 만들 수 없기 때문에 없앨 수 없다.
따라서 위 예시에서 없앨 수 있는 블록은 최대 2개이다.
보드 위에 놓인 블록의 상태가 담긴 2차원 배열 board가 주어질 때, 검은 블록을 떨어뜨려 없앨 수 있는 블록 개수의 최댓값을 구하라.
입력 및 출력
제한사항
- board는 블록의 상태가 들어있는 N x N 크기 2차원 배열이다.
- N은 4 이상 50 이하다.
- board의 각 행의 원소는 0 이상 200 이하의 자연수이다.
- 0 은 빈 칸을 나타낸다.
- board에 놓여있는 각 블록은 숫자를 이용해 표현한다.
- 잘못된 블록 모양이 주어지는 경우는 없다.
- 모양에 관계 없이 서로 다른 블록은 서로 다른 숫자로 표현된다.
- 예를 들어 문제에 주어진 예시의 경우 다음과 같이 주어진다.
입출력 예
| board | result |
| [[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,4,0,0,0],[0,0,0,0,0,4,4,0,0,0],[0,0,0,0,3,0,4,0,0,0],[0,0,0,2,3,0,0,0,5,5],[1,2,2,2,3,3,0,0,0,5],[1,1,1,0,0,0,0,0,0,5]] | 2 |
풀이
풀이 후에 numpy 라이브러리를 사용한 다른 분들의 풀이를 보았는데, 확실히 배열을 다루는 문제이다 보니 이런 문제에서 numpy가 큰 효용성을 지니는 걸 체감할 수 있었다. 코드의 깔끔함이라던가 실제 연산 속도라던가... 다만 가급적 파이썬 내장 기본 라이브러리로만 풀이하는 게 나을 것 같아 numpy를 이용한 풀이는 지양해야겠다싶다.
핵심 알고리즘은 '어떠한 블록이 그 시점에 제거될 수 있는지 계속 검사하는 것'이다. 만약 제거될 수 있는 블록이 더 없다면(즉 한 번의 순회 후 블록에 변동이 없다면) 그 시점에서 알고리즘을 멈추고 답을 출력하면 된다. 또한 '제거될 수 있는 상태'는 다음과 같이 정의해볼 수 있다.
- 블록의 최소 직사각형을 먼저 구한다. 최소 직사각형은 (블록의 최대 x좌표- 최소 x좌표)를 밑변으로, (블록의 최대 y좌표-최소 y좌표)를 높이로 가진다. 이 최소 직사각형에서 현재 블록에 존재하지 않는 좌표(board상의 number가 현재 블록과 다른 좌표)가 검사 대상이다.
- 이 검사 대상 좌표들이 모두 채워질 수 있다면 제거될 수 있는 상태이다. 검은 블록은 y=0 좌표로부터 점점 y축이 증가하는 방향으로 이동 가능하므로(즉 '떨어진다'), 검사 대상 좌표에 검은 블록이 도달할 수 있는 상태여야한다. 즉 모든 검사 대상 좌표를 기준으로, 같은 x좌표와 같거나 작은 y좌표의 모든 칸(즉 위쪽의 모든 칸)이 비어있어야 한다.
제거될 수 있는 상태의 블록들을 제거하고 board를 업데이트하면 된다.
- dfs : board를 순회하며 board 내의 블록에 해당하는 좌표를 찾는 함수. DFS를 이용하였다. 좌표 리스트인 block을 반환한다.
- min_rectangle : 앞서 말한 알고리즘의 최소 직사각형을 구하는 함수. dfs 함수를 통해 찾은 block 리스트를 이용한다. 앞선 알고리즘의 검사 대상 좌표들을 저장한다. (지금 생각해 보니 검사 대상 좌표들'만'을 저장하는 게 더 효율적일 것 같다)
- find_blocks : board 전체를 순회하며, dfs와 min_rectangle 함수를 이용해 block들을 구하는 함수. block의 리스트인 block_list를 반환한다.
- is_block_enable : block 내의 모든 검사대상 좌표들이 제거될 수 있는 상태인지 검사하는 함수.
- check_all_blocks : block_list를 순회하며, 각 block이 제거될 수 있는지 is_block_enable함수를 통해 검사한다. 만약 제거될 수 있다면 board를 업데이트하고, 그렇지 않으면 새로운 block_list에 담아 반환한다. 제거된 block 수 역시 반환한다.
- solution : 메인함수. find_blocks 함수로 block을 업데이트하고, 반복문을 통해 check_all_blocks로 block을 업데이트한다. 만약 업데이트할 block이 없다면(제거된 block 수가 0이라면) 반복문을 탈출한다.
풀이 코드
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def dfs(board, x, y, board_num, visited) :
block = [(x, y, 1)]
n = len(board)
q = [(x, y)]
visited[y][x] = True
while q :
x, y = q.pop()
for i in range(4) :
ax, ay = x + dx[i], y + dy[i]
if -1 < ax < n and -1 < ay < n and board[ay][ax] == board_num and not visited[ay][ax] :
block.append((ax, ay, 1))
visited[ay][ax] = True
q.append((ax, ay))
return block
def min_rectangle(board, board_num, block) :
x_list = sorted([ coord[0] for coord in block ])
y_list = sorted([ coord[1] for coord in block ])
for i in range(y_list[0], y_list[-1]+1) :
for j in range(x_list[0], x_list[-1]+1) :
if board[i][j] != board_num :
block.append((j, i, 0))
def find_blocks(board):
n = len(board)
visited = [[False]*n for _ in range(n)]
block_list = list()
for i in range(n) :
for j in range(n) :
if not visited[i][j] and board[i][j] :
block = dfs(board, j, i, board[i][j], visited)
min_rectangle(board, board[i][j], block)
block_list.append(block)
return block_list
def is_block_enable(board, block) :
for x, y, check in block :
if check == 1 :
continue
for i in range(y, -1, -1) :
if board[i][x] != 0 :
return False
return True
def check_all_blocks(board, block_list) :
if not block_list :
return 0, []
n = len(board)
block_num = len(block_list)
new_block_list = list()
cnt = 0
for idx, block in enumerate(block_list) :
if is_block_enable(board, block) :
for x, y, _ in block :
board[y][x] = 0
cnt += 1
continue
new_block_list.append(block)
return cnt, new_block_list
def solution(board):
block_list = find_blocks(board)
answer = 0
while True :
cnt, block_list = check_all_blocks(board, block_list)
answer += cnt
if cnt == 0 :
break
return answer
'PS > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 미로 탈출 (Python) (0) | 2023.02.21 |
|---|---|
| [프로그래머스] 올바른 괄호 개수 (Python) (0) | 2023.02.20 |
| [프로그래머스] 숫자 타자 대회 (Python) (0) | 2023.02.13 |
| [프로그래머스] 셔틀버스 (Python) (0) | 2023.02.11 |
| [프로그래머스] 카드 짝 맞추기 (Python) (0) | 2023.02.07 |
소중한 공감 감사합니다