Problem : https://school.programmers.co.kr/learn/courses/30/lessons/181186
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
Status : Solved
Time : 01:14:46
더보기
정우는 예술적 감각이 뛰어난 타일공입니다. 그는 단순한 타일을 활용하여 불규칙하면서도 화려하게 타일링을 하곤 합니다.
어느 날 정우는 가로 길이 n, 세로 길이 3 인 판을 타일링하는 의뢰를 맡았습니다. 아방가르드한 디자인 영감이 떠오른 정우는 다음과 같은 두 가지 종류의 타일로 타일링을 하기로 결정했습니다.

각 타일은 90도씩 회전할 수 있으며 타일의 개수는 제한이 없습니다.
n이 주어졌을 때, 이 두 가지 종류의 타일로 n x 3 크기의 판을 타일링하는 방법의 수를 return 하도록 solution 함수를 완성해주세요.
더보기
제한사항
- 1 ≤ n ≤ 100,000
- 결과는 매우 클 수 있으므로 1,000,000,007 로 나눈 나머지를 return합니다.
입출력 예
LV 3 매운맛. 타일링 DP 문제에 최적화 과정을 곁들여야 한다.
이 문제를 풀기 위해 고려해야 할 것은 크게 두 가지이다.
1. 단위 묶음의 경우의 수 구하기
타일링 문제의 단골이다만, 단위 묶음의 경우의 수를 모두 다 구해 보아야 한다. 이 문제에서의 단위 묶음이란, 더 이상 세로로 쪼 수 없는 묶음을 의미한다.



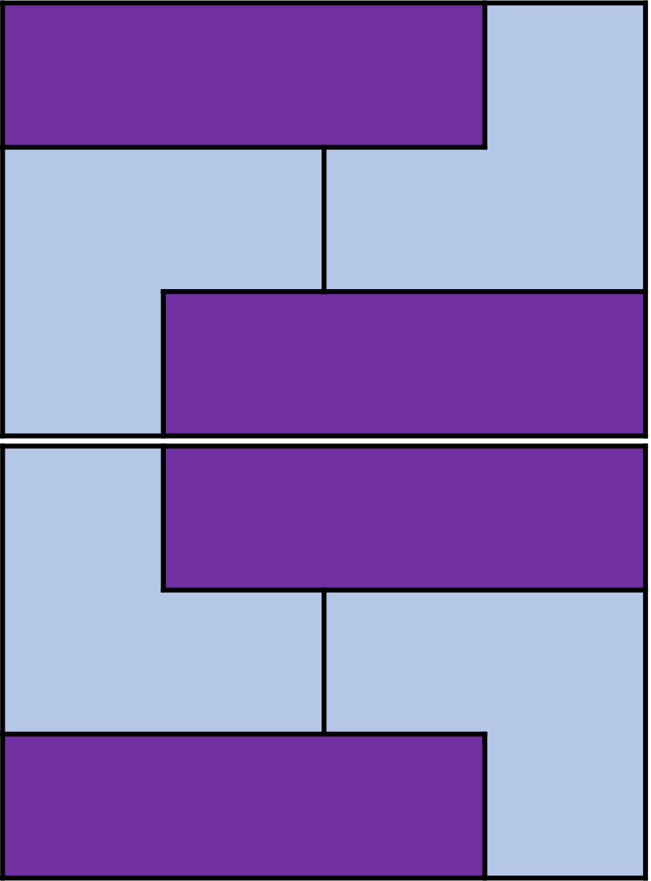


더 잘 생각해 보면, 7, 8, 9... x3은 4, 5, 6의 경우에서 3개의 1x3 타일을 중간에 끼워넣음으로써 구현할 수 있다. 이런 규칙성을 갖고 DP 점화식을 세워보자. dp[i]를 i x 3 면적의 타일을 칠하는 경우의 수라고 생각할 때...

가 된다. 우선, 이 방식대로 재귀적으로 풀이할 수도 있다.
문제는 이 방식에서 시간복잡도는 O(N^2)이 되므로 필연적으로 시간 초과가 발생한다!
2. DP 그룹화하기
앞선 식을 돌이켜 생각해보자. 우리는 먼저, 지난 i-1번째의 합을 저장해 둘 수 있다. 이를 토대로 묶어보면...

여기서 더 나아갈 수 있을 것 같다! 3의 배수에 따라 또한 재귀적으로 더해지므로, i에 3을 나눴을 때의 나머지와 같은(즉 같은 초기항과 공차를 가지는) 합도 저장해 둘 수 있을 것 같다! 이를 다시 러프하게 나타내보자.

마지막으로, i x 3의 단위 묶음을 그대로 사용하는 경우도 고려해주자.

즉 4개의 part로 나뉠 수 있으며, 4개 part 각각은 접근에 O(N)이 소요된다. 즉 O(N^2)이 아닌 O(N)시간복잡도 안에 모든 처리를 할 수 있다!
LV4를 주기엔 조금 부족한 건 알겠는데, LV3에 있기엔 조금 많이 빡센 문제였던 것 같다..!
풀이 코드
def solution(n):
if n < 4 :
return [0, 1, 3, 10][n]
MOD = 1000000007
dp = [0]*(n+1)
dp[1] = 1
dp[2] = 3
dp[3] = 10
partial_dp = [10, 1, 3]
dp_sum = sum(partial_dp)
for i in range(4, n+1) :
_add = 2 if i % 3 else 4
dp[i] = (dp_sum*2 % MOD - dp[i-1] + partial_dp[i%3]* 2 % MOD + dp[i-3] + _add) % MOD
dp_sum = (dp_sum + dp[i]) % MOD
partial_dp[i%3] = (partial_dp[i%3] + dp[i]) % MOD
return dp[n]
 풀이 완료!
풀이 완료!