[프로그래머스/LV5] 시험장 나누기 (Python)
- -
Problem : https://school.programmers.co.kr/learn/courses/30/lessons/81305#
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
Status : Solved
Time : 01:20:30
문제 설명
카카오 인턴을 선발하는 코딩 테스트 시험장이 하나의 이진 트리 형태로 연결되어 있습니다. 아래 그림은 12개의 시험장이 연결된 예시입니다.
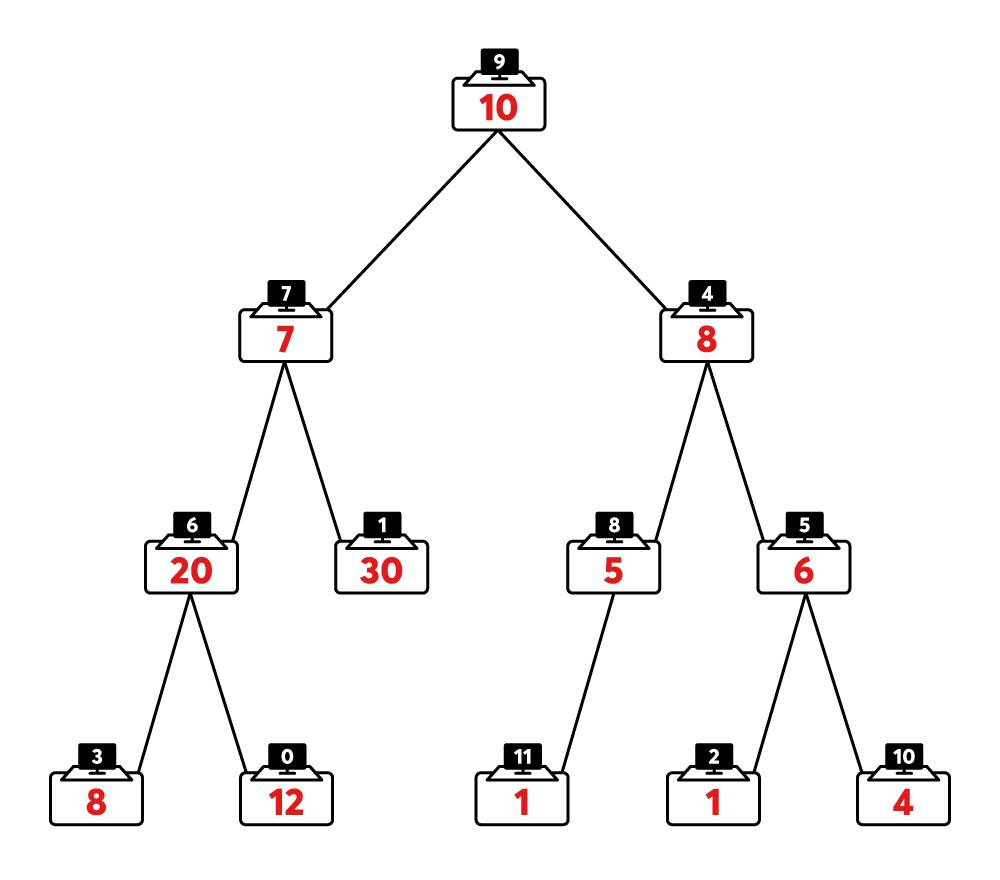
- 하나의 노드는 하나의 시험장을 나타냅니다.
- 검은 바탕의 흰 숫자는 해당 시험장의 고유 번호(ID)를 나타냅니다.
- 2-1. 시험장이 n개 있다면, 시험장의 고유 번호는 0부터 n-1까지 부여됩니다.
- 노드 안의 빨간 숫자는, 해당 시험장의 응시자 수를 나타냅니다.
- 3-1. 위의 그림에서, 9번 시험장에는 10명, 4번 시험장에는 8명, 6번 시험장에는 20명의 응시자가 시험을 볼 예정입니다.
- 노드 사이의 간선은 해당 시험장이 연결되어 있음을 의미합니다.
- 4-1. 위의 그림에서, 9번 시험장은 7번 시험장과, 7번 시험장은 6번 시험장과 연결되어 있습니다.
코딩 테스트를 총괄하는 무지는 안정적인 시험을 위해, 시험장에서 오는 트래픽을 k개의 그룹으로 나누어 각 그룹별 서버로 분산시키기로 하였습니다. 시험장 사이를 연결한 간선들 중 k-1개를 끊어서 시험장을 k 개의 그룹으로 나눌 계획입니다. 이때, 그룹별 최대 트래픽을 최소화하기 위하여 가장 큰 그룹의 인원을 최소화시켜야 합니다.
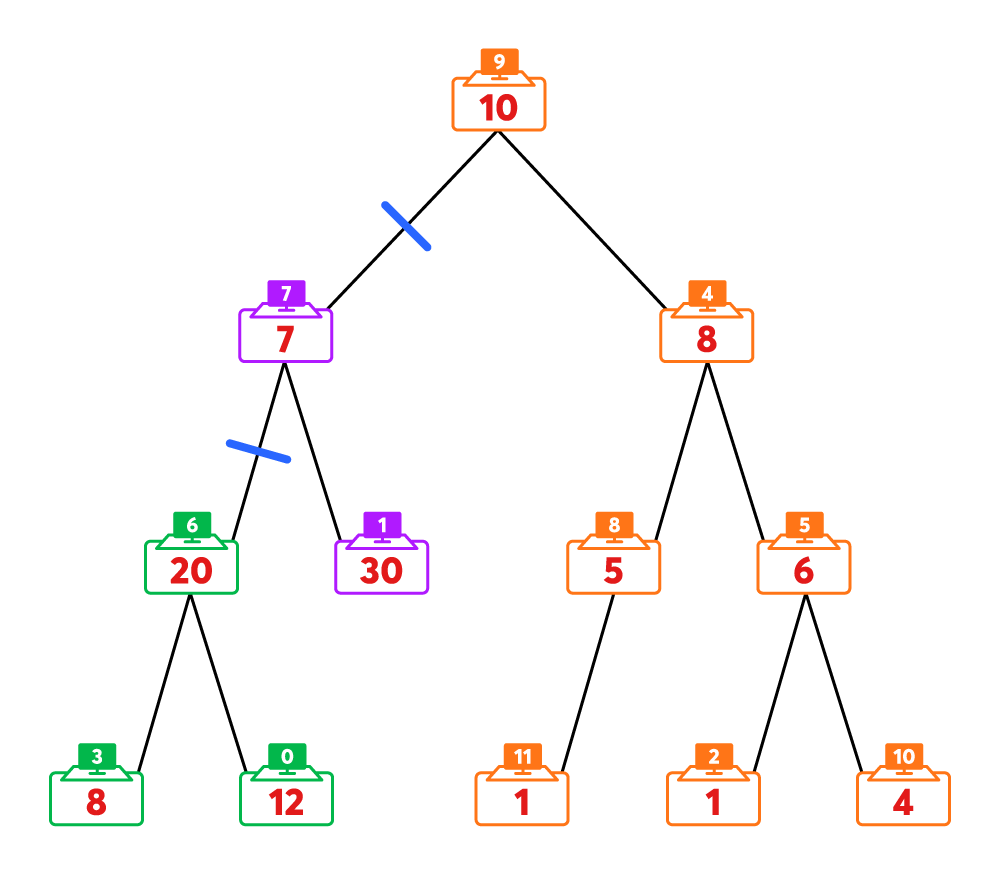
위의 그림에서 7번과 6번 시험장을 잇는 간선을 끊고, 9번과 7번 시험장을 잇는 간선을 끊는다면, 전체 시험장은 3개의 그룹으로 나누어집니다.
- 주황색 노드로 표시된 A그룹의 인원은 35명(10+8+5+6+1+1+4)
- 보라색 노드로 표시된 B그룹의 인원은 37명(7+30)
- 녹색 노드로 표시된 C그룹의 인원은 40명(20+8+12)
즉, 인원이 가장 많은 그룹은 40명입니다. 다른 어떤 방법으로 시험장을 3개의 그룹으로 나눈다고 해도, 인원이 가장 많은 그룹의 인원이 40명 미만이 되도록 나눌 수는 없습니다.
나눌 그룹의 수를 나타내는 정수 k, 각 시험장의 응시자 수를 나타내는 1차원 정수 배열 num, 시험장의 연결 상태를 나타내는 2차원 정수 배열 links가 매개변수로 주어집니다. 인원이 가장 많은 그룹의 인원이 최소화되도록 k개의 그룹으로 나누었을 때, 최소화된 최대 그룹의 인원을 return 하도록 solution 함수를 완성해주세요.
입력 및 출력
제한사항
- 1 ≤ k ≤ 10,000
- k ≤ num의 길이 ≤ 10,000
- num[i]에는 i번 시험장의 응시자 수가 담겨있습니다.
- 1 ≤ num의 원소 ≤ 10,000
- links의 길이 = num의 길이
- links의 i번째 행은 i번 노드(시험장)의 [왼쪽 자식 노드 번호, 오른쪽 자식 노드 번호]입니다.
- 해당 위치에 자식 노드가 없는 경우 -1이 담겨있습니다.
- 잘못된 노드 번호나, 하나의 이진 트리 구조가 아닌 입력은 주어지지 않습니다.
- links의 i번째 행은 i번 노드(시험장)의 [왼쪽 자식 노드 번호, 오른쪽 자식 노드 번호]입니다.
정확성 테스트 케이스 제한 사항
- 1 ≤ k ≤ 20
- k ≤ num의 길이 ≤ 20
효율성 테스트 케이스 제한 사항
- 주어진 조건 외 추가 제한사항 없습니다.
입출력 예
| k | num | links | result |
| 3 | [12, 30, 1, 8, 8, 6, 20, 7, 5, 10, 4, 1] | [[-1, -1], [-1, -1], [-1, -1], [-1, -1], [8, 5], [2, 10], [3, 0], [6, 1], [11, -1], [7, 4], [-1, -1], [-1, -1]] | 40 |
| 1 | [6, 9, 7, 5] | [[-1, -1], [-1, -1], [-1, 0], [2, 1]] | 27 |
| 2 | [6, 9, 7, 5] | [[-1, -1], [-1, -1], [-1, 0], [2, 1]] | 14 |
| 4 | [6, 9, 7, 5] | [[-1, -1], [-1, -1], [-1, 0], [2, 1]] | 9 |
풀이
완전 탐색으로 풀게 되면, 최대 노드 수 및 절단 수가 10000을 넘으므로 당연히 시간 초과를 겪게 된다. 처음에는 DP로 풀이해보려 했었는데, 결론만 먼저 말하자면 이분 탐색을 적용하는 게 정답이었다.
이 문제를 '절단 지점'에 포커스를 놓고 문제를 풀이하게 되면 접근이 어렵다. 대신, 주어진 k-1이내에 최대 x의 크기로 절단할 수 있는 최솟값을 구하는 문제로 생각해 보자. x값은 [num의 최댓값, num의 총합]만큼의 범위에서 탐색을 진행할 수 있으며, 이를 이분 탐색으로 풀어 볼 수 있다. num의 원소의 최댓값은 10000 = 1e4, 그리고 num의 길이 역시 10000이므로, 최대 범위 N는 약 [1, 1e8]으로 잡을 수 있으며, 이는 이분 탐색의 시간복잡도인 O(NlogN) 내에서 해결 가능하다.
- find_root : 탐색을 시작하기에 앞서, 루트 노드를 먼저 탐색해야 한다. 각 방문하지 않은 노드를 만날 때마다 노드를 저장하고 DFS로 방문점을 업데이트한다. 마지막으로 저장된 노드가 루트 노드가 된다. (DFS가 수행된다는 의미는 현재 노드가 이전에 저장된 노드보다 더 깊이가 얉음을 의미한다)
- search : 현재 주어진 제한합 이내로 최소 절단을 위해 트리를 재귀적으로 탐색한다. 현재 노드에서 오른쪽 서브트리, 왼쪽 서브트리를 탐색한 후, 양쪽의 절단값과 양쪽의 부분합을 전달받는다.
- 만약 노드값 + 왼쪽 부분합 + 오른쪽 부분합이 현재 제한합보다 작거나 같다면, 이 노드에서 절단은 불필요하므로 양쪽의 절단값과 위의 모든 값의 합을 반환한다.
- 그렇지 않다면, 왼쪽 부분합과 오른쪽 부분합 중 작은 값을 현재 제한합과 비교한다. 만약 작거나 같아면, 한 번의 절단이 필요하므로 양쪽의 절단값 + 1, 그리고 현재 노드값과 둘 중 작은 값의 합을 반환한다.
- 두 경우 모두 해당되지 않는다면, 두 리프 노드를 전부 절단해야 한다는 의미이다. 따라서 양쪽의 절단값 + 2, 그리고 현재 노드값만을 반환한다.
- binary_search : 이분 탐색 함수. start와 end를 초기값을 전달받아, search 함수를 통해 필요한 전체 절단값을 구한다. 이 절단값이 목표 절단값보다 작거나 같다면, 조건을 만족한다는 의미이므로 result값 및 end값을 업데이트한다. 그렇지 않다면 start값을 업데이트한다. 모든 탐색이 종료한 후 result값을 반환한다.
- solution : 메인함수. find_root로 루트 노드를 구하고, start, end값을 구한 후 binary_search 함수로 해답을 구하여 반환한다.
풀이 코드
import sys
sys.setrecursionlimit(int(1e6))
def find_root(links) :
length = len(links)
visited = [False]*length
for i in range(length) :
if not visited[i] :
result = i
q = [i]
visited[i] = 0
while q :
node = q.pop()
for leaf in links[node] :
if leaf > -1 and not visited[leaf] :
visited[leaf] = True
q.append(leaf)
return result
def search(node, target, num, links) :
if node == -1 :
return 0, 0
left, right = links[node]
left_cnt, left_val = search(left, target, num, links)
right_cnt, right_val = search(right, target, num, links)
tot_cnt = left_cnt + right_cnt
result_sum = left_val + right_val + num[node]
if result_sum <= target :
return tot_cnt, result_sum
if min(left_val,right_val) + num[node] <= target :
return tot_cnt + 1, min(left_val,right_val) + num[node]
return tot_cnt + 2, num[node]
def binary_search(root, start, end, k, num, links) :
result = end
while start <= end :
mid = (start + end) // 2
div_cnt, _ = search(root, mid, num, links)
if div_cnt > k-1 :
start = mid+1
else :
result = min(result, mid)
end = mid-1
return result
def solution(k, num, links):
length = len(links)
root = find_root(links)
start, end = max(num), sum(num)
answer = binary_search(root, start, end, k, num, links)
return answer
다들 LV5 문제 중에선 쉽다고들 하시는데, 나는 아직 갈 길이 멀었나보다 ㅠㅠ
'PS > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/LV4] 매출 하락 최소화 (Python) (0) | 2023.03.11 |
|---|---|
| [프로그래머스/LV5] 방의 개수 (Python) (0) | 2023.03.10 |
| [프로그래머스/LV4] 미로탈출 (Python) (0) | 2023.03.08 |
| [프로그래머스/LV4] 쌍둥이 빌딩 숲 (0) | 2023.03.07 |
| [프로그래머스/LV3] 110 옮기기 (Python) (0) | 2023.03.06 |
소중한 공감 감사합니다